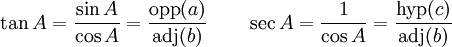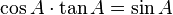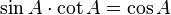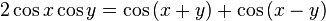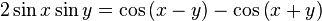Ariyaporn Phatanasing: 2014

ประวัติของตรีโกณมิติ

นักคณิตศาสตร์มุสลิมในยุคกลาง (หรือยุคมืด ตามคำเรียกของชาวยุโรป) มีส่วนเป็นอย่างมากในการพัฒนาและอุทิศผลงานในคณิตศาสตร์สาขาตรีโกณมิติ โดยพวกเขาได้รับแนวคิดพื้นฐานมาจาก

ตำราคณิตศาสตร์อินเดียที่ชื่อ Sūrya Siddhānta (สูรยสิทธานตะ)
ตำราอัลมาเกส (เป็นภาษาอาหรับแปลว่ายิ่งใหญ่ที่สุด แสดงให้เห็นว่านักคณิตศาสตร์อาหรับยกย่องหนังสือเล่มนี้มาก) ของทอเลมีนักคณิตศาสตร์ที่มีชื่อเสียงชาวกรีก ; และ
ตำราสเฟียริก ของเมเนลาอุสนักคณิตศาสตร์ชาวกรีกเช่นกัน

อย่างไรก็ตาม ถึงแม้ว่านักคณิตศาสตร์กรีกและอินเดียจะมีบทบาทในการพัฒนาตรีโกณมิติ แต่ทว่านักประวัติศาสตร์คณิตศาสตร์หลายท่าน ได้ให้เกียรตินักคณิตศาสตร์อาหรับว่า เป็นผู้พัฒนาความรู้ในสาขานี้อย่างแท้จริง

สำหรับ ประเทศไทยนั้น ก็มีศาสตร์ตรีโกณมิติเข้ามาตั้งแต่สมัยสุโขทัย ผ่านทางคัมภีร์ สุริยยาตร์ สำหรับคำนวณหาตำแหน่งพระอาทิตย์และพระจันทร์ และปรากฏการณ์ข้างขึ้นข้างแรม (เพียร) โดยปรากฏตาราง SINE ทุกๆ มุม 15 องศา เรียกว่า ตารางฉายา ส่วน COSINE จะใช้หลักการเทียบจากตารางฉายา เรียกว่า โกฏิฉายา

ตรีโกณมิติในปัจจุบัน

ปัจจุบัน มีการนำตรีโกณมิติไปใช้ในงานสาขาต่าง ๆ เช่น เป็นเทคนิคในการสร้างรูปสามเหลี่ยม ซึ่งใช้ในวิชาดาราศาสตร์เพื่อวัดระยะทางของดาวที่อยู่ใกล้ ในภูมิศาสตร์ใช้วัดระยะทางระหว่างหลักเขตที่ดิน และใช้ในดาวเทียมนำทาง งานที่มีการใช้ประโยชน์จากตรีโกณมิติ ได้แก่ ดาราศาสตร์ (และการนำทางในมหาสมุทร บนเครื่องบิน และในอวกาศ) ,ทฤษฎีดนตรี, สวนศาสตร์, ทัศนศาสตร์, การวิเคราะห์ตลาดการเงิน, อิเล็กทรอนิกส์, ทฤษฎีความน่าจะเป็น, สถิติศาสตร์, ชีววิทยา, การสร้างภาพทางการแพทย์ (การกราดภาพตัดขวางใช้คอมพิวเตอร์ช่วย (CAT scans) และ คลื่นเสียงความถี่สูง) ,เภสัชศาสตร์, เคมี, ทฤษฎีจำนวน (รวมถึง วิทยาการเข้ารหัสลับ) , วิทยาแผ่นดินไหว, อุตุนิยมวิทยา, สมุทรศาสตร์, วิทยาศาสตร์กายภาพสาขาต่างๆ, การสำรวจพื้นดิน และภูมิมาตรศาสตร์, สถาปัตยกรรม, สัทศาสตร์, เศรษฐศาสตร์, วิศวกรรมไฟฟ้า, วิศวกรรมเครื่องกล, วิศวกรรมโยธา, เรขภาพคอมพิวเตอร์, การทำแผนที่, ผลิกศาสตร์

เกี่ยวกับตรีโกณมิติ

รูปสามเหลี่ยมสองรูปจะเรียกว่าคล้ายกัน ถ้ารูปหนึ่งสามารถขยายได้เป็นอีกรูปหนึ่ง และจะเป็นกรณีนี้ก็ต่อเมื่อมุมที่สมนัยกันมีขนาดเท่ากัน ตัวอย่างเช่น รูปสามเหลี่ยมสองรูปที่มีมุมร่วมกันมุมหนึ่ง และด้านที่ตรงข้ามกับมุมนั้นขนานกัน เป็นข้อเท็จจริงว่ารูปสามเหลี่ยมที่คล้ายกัน ด้านแต่ละด้านจะเป็นสัดส่วนกัน นั่นคือ ถ้าด้านที่ยาวที่สุดของรูปสามเหลี่ยมหนึ่ง ยาวเป็นสองเท่าของด้านที่ยาวที่สุดของรูปสามเหลี่ยมที่คล้ายกัน จะกล่าวได้ว่า ด้านที่สั้นที่สุดจะยาวเป็นสองเท่าของด้านที่สั้นที่สุดของอีกรูปสามเหลี่ยม และด้านที่ยาวปานกลางก็จะเป็นสองเท่าของอีกรูปสามเหลี่ยมเช่นกัน อัตราส่วนระหว่างด้านที่ยาวที่สุดและด้านที่สั้นที่สุดของรูปสามเหลี่ยมแรก จะเท่ากับ อัตราส่วนระหว่างด้านที่ยาวที่สุดและด้านที่สั้นที่สุดของรูปสามเหลี่ยมอีกรูปด้วย

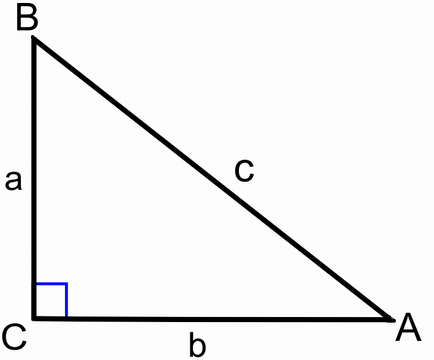
จากข้อเท็จจริงเหล่านี้ เราจะนิยามฟังก์ชันตรีโกณมิติ เริ่มต้นด้วยรูปสามเหลี่ยมมุมฉาก ซึ่งเป็นรูปสามเหลี่ยมซึ่งมีมุมฉากหนึ่งมุม (90 องศา หรือ π/2 เรเดียน) ด้านที่ยาวที่สุดในรูปสามเหลี่ยมใดๆจะอยู่ตรงข้ามกับมุมที่ใหญ่ที่สุด แต่เพราะว่าผลรวมของมุมภายในรูปสามเหลี่ยมเท่ากับ 180 องศา หรือ π เรเดียน ดังนั้นมุมที่ใหญ่ที่สุดในรูปสามเหลี่ยมนี้คือมุมฉาก ด้านที่ยาวที่สุดในรูปสามเหลี่ยมจึงเป็นด้านที่ตรงข้ามกับมุมฉาก เรียกว่า ด้านตรงข้ามมุมฉาก

นำรูปสามเหลี่ยมมุมฉากมาสองรูปที่มีมุม A ร่วมกัน รูปสามเหลี่ยมทั้งสองนี้จะคล้ายกัน และอัตราส่วนของด้านตรงข้ามมุม A ต่อด้านตรงข้ามมุมฉาก จะเท่ากันทั้งสองรูป มันจะเป็นจำนวนระหว่าง 0 ถึง 1 ขึ้นอยู่กับขนาดของมุม A เท่านั้น เราเรียกว่า ไซน์ของ A และเขียนด้วย sin (A) ในทำนองเดียวกัน เรานิยาม โคไซน์ของ A คืออัตราส่วนระหว่าง ด้านประชิดมุม A ต่อด้านตรงข้ามมุมฉาก

$\sin A = {\mbox{opp} (a) \over \mbox{hyp} (c) } \qquad \cos A = {\mbox{adj} (b) \over \mbox{hyp} (c) }$

ฟังก์ชันเหล่านี้เป็นฟังก์ชันตรีโกณมิติที่สำคัญ ฟังก์ชันอื่นๆสามารถนิยามโดยใช้อัตราส่วนของด้านต่างๆของรูปสามเหลี่ยม แต่มันก็สามารถเขียนได้ในรูปของ ไซน์ และ โคไซน์ ฟังก์ชันเหล่านี้คือ แทนเจนต์, ซีแคนต์, โคแทนเจนต์, และ โคซีแคนต์

$\tan A = {\sin A \over \cos A} = {\mbox{opp} (a) \over \mbox{adj} (b) } \qquad \sec A = {1 \over \cos A} = {\mbox{hyp} (c) \over \mbox{adj} (b) }$

$\cot A = {\cos A \over \sin A} = {\mbox{adj} (b) \over \mbox{opp} (a) } \qquad \csc A = {1 \over \sin A} = {\mbox{hyp} (c) \over \mbox{opp} (a) }$

วิธีจำ ไซน์ โคไซน์ แทนเจนต์ อย่างง่ายๆคือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด (ไซน์-ด้านตรงข้าม-ด้านตรงข้ามมุมฉาก โคไซน์-ด้านประชิด-ด้านตรงข้ามมุมฉาก แทนเจนต์-ด้านตรงข้าม-ด้านประชิด)

ที่ผ่านมา ฟังก์ชันตรีโกณมิติถูกนิยามขึ้นสำหรับมุมระหว่าง 0 ถึง 90 องศา (0 ถึง π/2 เรเดียน) เท่านั้น หากใช้วงกลมหนึ่งหน่วย จะขยายได้เป็นจำนวนบวกและจำนวนลบทั้งหมด (ดูใน ฟังก์ชันตรีโกณมิติ)

ครั้งหนึ่ง ฟังก์ชันไซน์และโคไซน์ถูกจัดลงในตาราง (หรือคำนวณด้วยเครื่องคิดเลข) ทำให้ตอบคำถามทั้งหมดเกี่ยวกับรูปสามเหลี่ยมใดๆได้อย่างแท้จริง โดยใช้กฎไซน์ และ กฎโคไซน์

กฎเหล่านี้สามาถใช้ในการคำนวณมุมที่เหลือและด้านของรูปสามเหลี่ยมได้ เมื่อรู้ความยาวด้านสองด้านและขนาดของมุมหนึ่งมุม หรือรู้ขนาดของมุมสองมุมและความยาวของด้านหนึ่งด้าน หรือ รู้ความยาวของด้านทั้งสามด้าน

นักคณิตศาสตร์บางคนเชื่อว่าตรีโกณมิติแต่เดิมนั้น ถูกประดิษฐ์ชึ้นเพื่อใช้คำนวณนาฬิกาแดด ซึ่งมักเป็นโจทย์ในหนังสือเก่าๆ มันมีความสำคัญมากในเรื่องการสำรวจ

รายชื่อเอกลักษณ์ตรีโกณมิติ

เอกลักษณ์ตรีโกณมิติ คือการเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม

เมื่อกำหนด A เป็นขนาดของมุมใดๆ $(0\le A\le 2\pi)$ จะได้

$\sin A \cdot \csc A = 1$

$\cos A \cdot \sec A = 1$

$\tan A \cdot \cot A = 1$

$\cos A \cdot \tan A = \sin A$

$\sin A \cdot \cot A = \cos A$

$\sin^2 A + \cos^2 A = 1\,$

$\sec^2 A - \tan^2 A = 1\,$

$\csc^2 A - \cot^2 A = 1\,$

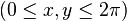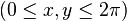เมื่อกำหนด x และ y เป็นขนาดของมุมใดๆ $(0\le x,y\le 2\pi)$ จะได้

$\sin \left(x+y\right)=\sin x \cos y + \cos x \sin y$

$\sin \left(x-y\right)=\sin x \cos y - \cos x \sin y$

$\cos \left(x+y\right)=\cos x \cos y - \sin x \sin y$

$\cos \left(x-y\right)=\cos x \cos y + \sin x \sin y$

$\tan \left(x+y\right)=\frac{\tan x + \tan y}{1 - \tan x \tan y}$

$\tan \left(x-y\right)=\frac{\tan x - \tan y}{1 + \tan x \tan y}$

$\sin x+\sin y=2\sin \left( \frac{x+y}{2} \right) \cos \left( \frac{x-y}{2} \right)$

$\sin x-\sin y=2\cos \left( \frac{x+y}{2} \right) \sin \left( \frac{x-y}{2} \right)$

$\cos x+\cos y=2\cos \left( \frac{x+y}{2} \right) \cos \left( \frac{x-y}{2} \right)$

$\cos x-\cos y=-2\sin \left( \frac{x+y}{2} \right)\sin \left( \frac{x-y}{2} \right)$

$\tan x+\tan y=\frac{\sin \left( x+y\right) }{\cos x\cos y}$

$\tan x-\tan y=\frac{\sin \left( x-y\right) }{\cos x\cos y}$

$\cot x+\cot y=\frac{\sin \left( x+y\right) }{\sin x\sin y}$

$\cot x-\cot y=\frac{-\sin \left( x-y\right) }{\sin x\sin y}$

$2\sin x \cos y=\sin \left(x+y\right) + \sin \left(x-y\right)$

$2\cos x \sin y=\sin \left(x+y\right) - \sin \left(x-y\right)$

$2\cos x \cos y=\cos \left(x+y\right) + \cos \left(x-y\right)$

$2\sin x \sin y=\cos \left(x-y\right) - \cos \left(x+y\right)$

$\sin 2x=2\sin x \cos x=\frac{2\tan x}{1+\tan^2 x}$

$\cos 2x=\cos^2 x - \sin^2 x=1-2\sin^2 x=2\cos^2 x-1=\frac{1-\tan^2 x}{1+\tan^2 x}$

$\tan 2x=\frac{2\tan x}{1-\tan^2 x}$

$\sin 3x=3\sin x - 4\sin^3 x$

$\cos 3x=4\cos^3 x - 3\cos x$

$\tan 3x=\frac{3\tan x - \tan^3 x}{1-3\tan x}$

สมาชิก

1.นายภาวุฒิ พิสูจน์จักรวาฬ ชั้น ม.6/1 เลขที่ 20

2.นายณัฐภัทร วิบูลย์ลักษณากุล ชั้น ม.6/1 เลขที่ 30

3.นางสาวชยุตา อินทร์พิทักษ์ ชั้น ม.6/1 เลขที่ 37

4.นางสาวณัฐสุดา รุ่งเรือง ชั้น ม.6/1 เลขที่ 39

5.นางสาวอริยาภร์ พัฒนสิงห์ ชั้น ม.6/1 เลขที่ 40

Ariyaporn Phatanasing

วันอังคารที่ 28 มกราคม พ.ศ. 2557

ตรีโกณมิติ วิชาคณิตศาสตร์